Buongiorno continuiamo oggi con la seconda parte sul percorso delle equazioni di primo grado. Le equazioni in generale sono un argomento fondamentale per la matematica e soprattutto per i nostri studenti. Come presentarle? Come affrontare i diversi approcci? Come può aiutarci una semplice programmazione al pc?
Continuiamo il nostro percorso di riflessione critica sulle equazioni di primo grado.
Buona lettura.
lezione 3: superare la difficoltà semantica
Ci sono vari studi, che dimostrano che molti studenti, sebbene abbiano capito l’algebra e la necessità di utilizzare le lettere, preferiscono utilizzare sempre il linguaggio verbale piuttosto che iconico o astratto.
Nelle prime due lezioni, abbiamo proposto la storia delle equazioni, abbiamo fatto capire lo sviluppo dell’incognita. Nella seconda lezione, in particolare, abbiamo proposto un metodo di risoluzione dandone una interpretazione geometrica e grafica .
Siamo certi che i ragazzi interpretano un problema semanticamente?
Viene loro assegnato il seguente problema dove manca il referente numerico.
“In un poligono regolare ciascun lato misura 5 cm. Come si può descrivere il
perimetro sapendo che il poligono ha y lati?”.
E un altro
“In una piramide quadrangolare VABCD il triangolo VAC è equilatero di lato l.
Determinare il volume”
In questa lezione vengono proposti i principi di equivalenza
Prendiamo in prestito alcuni concetti dalla fisica, in particolare sulle leve di 1 specie: le bilancie. Dopo aver sviluppato un iniziale registro iiconico, l’idea è di continuare su questo discorso e di mostrare ai ragazzi alcune bilancie
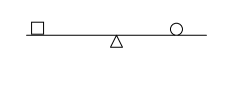
Problema 1. Se la figura rappresenta una bilancia in equilibrio come potreste esprimere a parole e con i simboli matematici la relazione tra i pesi dei due piatti?
Problema 2.Se la figura rappresenta una bilancia in equilibrio come potreste esprimere a parole e con i simboli matematici la relazione tra i pesi dei due piatti? Il quadrato rappresenta una scatola di zucchero.
Si passa al registro simbolico.
Vengono presentate altre due figure dove l’idea è fargli scrivere simbolo (non necessariamente x)= numero
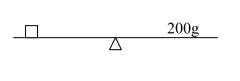
Qui vengono introdotti i concetti di uguaglianza, viene sottolineato il concetto di uguale.
Altro grafico
Problema 3: traduci a parole ciò che vedi sulla bilancia
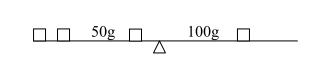
Proposta 3 scatole + 50 grammi pesano quanto uan scatola + 100grammi
3s + 50 = s + 100
I ragazzi sanno ben utilizzare i simboli (lo fanno anche con il cellulare) per scrivere.
E’ qui che il docente si inserisce: la bilancia, i problemi di uguaglianza, vengono riconosciuti come equazioni?
In una classe dove siano stati già presentate le equazioni di 1 grado, con i principi di equivalenza, la risposta è no.
Qui da noi invece per ora sono stati presentate le equazioni solo storicamente, come funzioni e non ancora algebricamente.
L’idea insomma è di presentare le equazioni algebriche, i 2 principi e le regole che ne derivano, come un metodo di risoluzione, alternativo a quello delle funzioni.
I principi possono così essere presentati
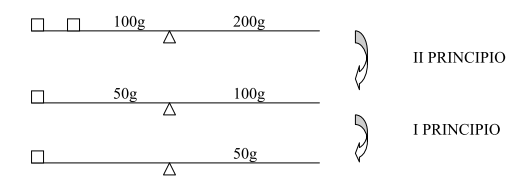
lezione 4 e 5: problemi ed esercizi
Nella lezione 4 e 5 vengono affrontati alcuni problemi inerenti alle equazioni
Problema 1: in un mese ho speso 35 euro di telefono effettuando 400 minuti di chiamate. Sapendo che il canone fisso mensile è di 10 euro, calcoliamo il costo al minuto di una telefonata.
Problema 2“vado al mercato con 70 €, quanti chili di un prodotto che costa 4 € al chilo posso comprare al massimo?”
Vengono svolti esercizi alla lavagna sia di problemi di geometria, sia di tipo numerico, sia equazioni prettamente algebriche
Problema 3
Una fattoria ha conigli e galline, sapendo che in totale ci sono 70 teste e 100 zampe, quante galline e conigli ci sono?
Problema 4
La scelta di tale equazione è motivata dal fatto che sono presenti prodotti notevoli e termini di secondo grado
lezione 6: verifica
Programmazione su excel
A B C D
|
Y=ax+b |
Y=cx+d |
|||
|
Dammi a |
Dammi b |
Dammi c |
Dammi d |
|
|
X |
y |
X |
Y |
|
|
-1 |
=a$2*A4+b$2 |
-1 |
=c$2*A4+d$2 |
Plot grafico |
|
0 |
trascina |
0 |
trascina |
|
|
1 |
1 |
programma in turbo pascal equazioni di primo grado
Program equ1gra;
uses Crt;
var a,b,c,d,x:real;
begin
writeln ('Questo programma risolve le equazioni di primo grado');
clrscr;
writeln('Inserisci i numeri dell''equazione per risolverla');
writeln('Scrivi il primo coefficente della x');
readln(a);
writeln('Scrivi il primo termine noto');
readln(b);
writeln('Scrivi il secondo coefficente della x');
readln (c);
writeln('Scrivi il secondo termine noto');
readln(d);
if(a-c)<>0 then
begin
x:=(d-b)/(a-c);
writeln('x: ',x:6:2);
end
else
begin
if(d-b)=0 then
begin
writeln('L''equazione è indeterminata');
end
else
begin
writeln('L''equazione è impossibile');
end;
end;
readln ;
end.
Articoli correlati
Didattica della matematica: le equazioni di primo grado, una riflessione critica parte 1
Bibbliografia
Arzarello F., Bazzini L., Chiappino G. (1994). L’algebra come strumento di pensiero.
Progetto strategico del C.N.R.: tecnologie e innovazioni didattiche. Quaderno n.6, Università di Pavia.
Chevallard Y. (1989). Arithmetique, Algebre, Modelisation. Aix-Marseille: Publications
de L’IREM.
Maracchia, Storia delle equazioni e dei sistemi di primo grado, Note della conferenza tenutasi a Castione(TI) il 28 agosto 2007, nell’ambito del corso di aggiornamentoper docenti di matematica di scuola media, rielaborate da Piero Antognini
Sfard A. (1991). On the dual nature of mathematical conceptions:Reflections on processes and objects on different sides of the same coin. Educational Studies in Mathematics, 22(1), 1-36.
Sfard A. (1992). The development of algebra. Confrontino historical and psychological perspectives, Algebra Working group, ICME 7. Quebec.
D’Amore B.(1999). Elementi di Didattica della Matematica. Bologna: Pitagora.
http://www.treccani.it/scuola/lezioni/in_aula/matematica/algebra/valenti.html le equazioni di 1 grado in Italia e altrove